Propiedades.
Las reglas hacen parte de todo en la vida, y en la potenciación se aplican como propiedades que nacen de los axiomas o verdades absolutas. Antes de mirar las propiedades, aclarare algunas cosas.
-Cuando hay dos números en un paréntesis elevados a la n, se aplica la propiedad distributiva.
( A x B ) elevado a la n = (A elevado a la n) (B elevado a la n)
( 3 x 2 ) elevado al cuadrado = (3 al cuadrado) (2 al cuadrado) = 9 x 4= 36
Como se evidencia anteriormente, se puede multiplicar el contenido del paréntesis y luego aplicar la potenciación, o sea multiplicar 3x2 y elevar el resultado al cuadrado.
-La potencia de base y exponente cero no existe.
-Cero elevado a la n, siempre sera cero (si n es diferente a cero).
Ya aclarado lo anterior, las propiedades de la potenciación son:
- Todo número elevado a la cero es igual a 1.
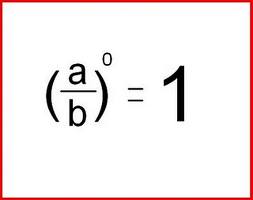
937°=1 0°= no se puede, acuerdense.
- Un número elevado a la 1 es igual a sí mismo.
b elevado a la 1= b 100 a la 1= 100 0 a la uno= 0
- Para multiplicar potencias que tienen la misma base, se suman las potencias y la base no cambia.
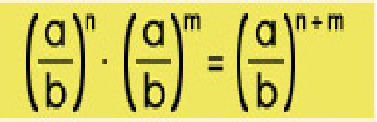
Por ejemplo 5 al cubo por 5 al cuadrado= 5 elevado a la 3+2= 5 a la 5
- Para divir potencias de igual base, se restan los exponentes y la base no cambia.
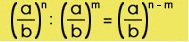
Por ejemplo 5 al cubo dividido 5 al cuadrado= 5 elevado a la 3-2= 5 a la 1 = 5
- Cuando hay una potencia elevada a otra potencia, se multiplican los exponentes y ya sabemos que pasa con la base, queda igual.
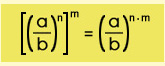
Una expresión con potencias enteras está simplificada si:
1.) No tiene exponentes negativos o cero.
2.) Los coeficientes son números primos.
3.) No faltan propiedades por aplicar ( Cada variable y cada número primo aparece una sola vez).
