Propiedades de la Radicación.

Sean m,n,k y l números naturales, a y b números cualquiera, entonces:

1.) Toda raíz puede ser expresada como exponente fraccionario, teniendo el índice como denominador del exponente.

                                            

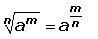
2.) Para simplicar radicales se necesita que el exponente y el índice sean iguales o el exponente mayor que el índice. Es necesario aclarar que deben estar multiplicando, si estan sumando no aplica, a menos de que el binomio sea completamente igual.

                                            

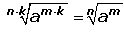
3.) Para introducir factores dentro del radical, se debe poner como exponente el índice, de modo que el valor del factor no cambie.

                                            

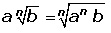
4.) Cuando dos radicales se estan multiplicando, y tienen el mismo índice, se lleva el contenido a un solo radical.

                                            

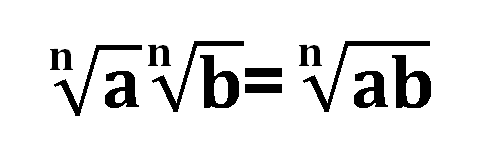
5.) Cuando dos radicales se estan dividiendo, y tienen el mismo índice, se lleva el contenido a un solo radical.

                                            

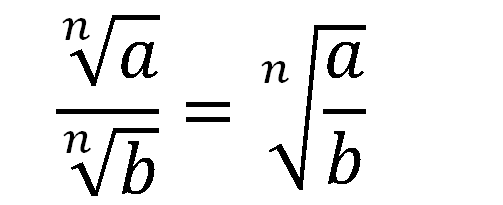
6.) Para multiplicar radicales con diferente índice, se multiplican los índices, se divide el resultado por el índice original de cada radical, y el resultado se multiplica por los exponentes para compensar el cambio de los índices.

                                            

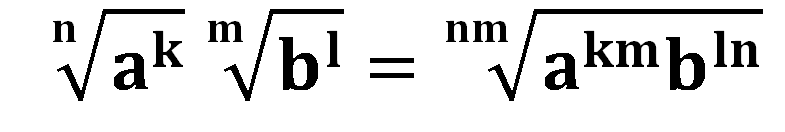
La anterior es una propiedad general, pero es mucho mas factible acudir al m.c.m ( minimo común multipo ) para llevar los índices a una igualdad. Al ser la radicación lo contrario de la potenciación, cada que uno cambia, el otro tambien cambia, es decir, si el índice se multiplica por 3, el exponente también se multiplica por 3, si el índice se divide "x" cantidad de veces, el exponente tambien debe dividirse "x" cantidad de veces. Por ejemplo el m.c.m de 4 y 6 es 12, la pregunta de oro es: ¿POR CUÁL NÚMERO DEBO MULTIPLICAR AL 4 PARA QUE LLEGUE A 12? y lo mismo con el 6. Correcto, la respuesta es 3 y 2 respectivamente, por esos dos números se debe multiplicar el exponente del factor interno del radical (en el radical que tiene como índice el 4 se debe multiplicar por 3 los exponentes internos y el que tiene como índice el 6 se multiplica por 2 los exponentes internos).

En videos se explica de la manera mas sencilla. Más adelante veremos lo facil que resulta ser.

 

7.) Para dividir radicales con diferente índice, se aplica exactamente el mismo método de la multiplicacion, la única diferencia es que el contenido se divide. 

                                           

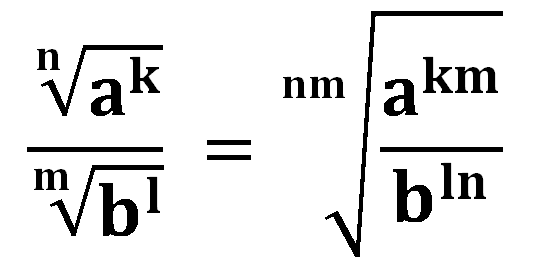
8.) Cuando un radical tiene potencia, se le atribuye el exponente a la cantidad subradical.

                                           

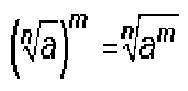
9.) En el caso de raíz de raíz, se multiplican los índices.

                                           

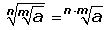
10.) Sí se están sumando "x" números acompañados de un radical igual, se suman los números y el radical no cambia.

                                        

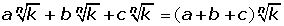
Supongamos que 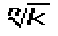 representa la palabra manzana, entonces tendríamos a manzanas+b manzanas+c manzanas, y cuanto seria eso? sencillo, a+b+c manzanas.

 

Se sabe que un radical esta simplificado solo cuando:

1.) El radicando contiene factores con potencias inferiores al índice.

2.) Las potencias de los factores del radicando y el índice del radical no tienen factores comunes.

 

Una expresión con potencias y radicales esta simplificada si:

1.) No contiene exponentes racionales.

2.) Cumple las condiciones de simplificación de  expresiones con potencias.

3.) Cumple las condiciones de simplificación de radicales.